La Lithopanspermie Interplanétaire
Contexte : L'énigme de nos origines et la connexion martienne.
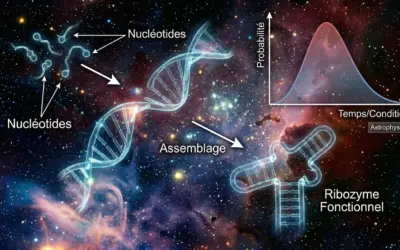
L'apparition de la vie sur Terre, ou AbiogenèseProcessus naturel par lequel la vie émerge à partir de matière non-vivante., est l'un des plus grands mystères de la science. Les archives fossiles indiquent que la vie est apparue très tôt, il y a environ 3,8 à 4,1 milliards d'années, presque immédiatement après que la Terre ait suffisamment refroidi pour posséder des océans liquides. Ce timing "trop parfait" trouble les scientifiques : comment une chimie aussi complexe a-t-elle pu émerger si vite dans un environnement aussi chaotique ?
C'est ici qu'intervient l'hypothèse de la PanspermieThéorie selon laquelle la vie se propage dans l'univers via des vecteurs célestes.. Cette théorie suggère que la Terre n'a pas nécessairement "inventé" la vie, mais qu'elle l'a "reçue". Si la soupe primordiale terrestre n'a pas eu le temps de mijoter, peut-être que la recette a été élaborée ailleurs ?
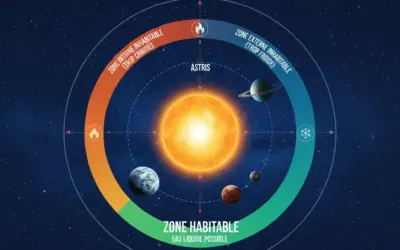
Mars est la suspecte numéro un. Il y a 4 milliards d'années, Mars était une planète bleue, chaude et humide, bien avant la Terre. Plus petite, elle a refroidi plus vite, offrant des conditions habitables des centaines de millions d'années avant notre propre planète. Le scénario de la LithopanspermieTransport de micro-organismes à l'intérieur de fragments rocheux éjectés d'une planète par impact. propose une histoire fascinante : la vie serait née sur Mars, puis, suite à des bombardements d'astéroïdes massifs, des fragments de croûte martienne contenant des microbes auraient été éjectés dans l'espace. Ces "arches de Noé" minérales auraient voyagé à travers le système solaire avant de s'écraser sur la Terre primitive, ensemençant nos océans stériles.
Dans cet exercice, nous n'allons pas faire de la science-fiction, mais de la physique. Nous allons vérifier si ce voyage épique est mécaniquement possible, biologiquement survivable et statistiquement plausible.
Remarque Pédagogique : L'Art de la Modélisation Scientifique
Cet exercice est conçu pour développer une compétence cruciale chez le futur scientifique : la capacité à relier des disciplines apparemment disjointes pour résoudre une énigme complexe.
- Interdisciplinarité Radicale : Vous allez marier la Mécanique Céleste (lois de Newton et Kepler régissant le mouvement des astres massifs) avec la Microbiologie (résistance des structures cellulaires et de l'ADN face à l'entropie). C'est le cœur même de l'Astrobiologie moderne.
- Esprit Critique & Paradoxe de Fermi : En calculant ces probabilités, nous touchons aux questions existentielles. Si le transport de la vie est "facile" physiquement, pourquoi l'Univers ne grouille-t-il pas de vie ? Cet exercice transforme une spéculation philosophique ("sommes-nous seuls ?") en un problème quantitatif concret ("quelle est la probabilité \(P\) ?").
- Maîtrise des Ordres de Grandeur : Vous allez manipuler des échelles de temps géologiques (millions d'années) et des distances astronomiques (millions de kilomètres), tout en considérant la fragilité microscopique d'une bactérie de quelques micromètres. Comprendre comment l'infiniment petit survit dans l'infiniment grand est un vertige intellectuel nécessaire pour appréhender notre place dans le cosmos.
- La Puissance de l'Approximation : Nous utiliserons des modèles simplifiés (orbites circulaires, décroissance exponentielle simple). L'objectif pédagogique n'est pas la précision absolue (impossible sans supercalculateur), mais l'obtention d'un ordre de grandeur correct pour valider ou réfuter la plausibilité du scénario.
Ne voyez pas les calculs qui suivent comme une corvée mathématique, mais comme les pièces d'un puzzle narratif qui raconte l'histoire potentielle de nos propres origines.
Objectifs Pédagogiques
À la fin de cet exercice, vous serez capable de :
-
1. Maîtriser l'Énergétique Gravitationnelle
Comprendre physiquement le concept de "puits de gravité". Vous apprendrez à calculer la vitesse de libération non pas comme une simple formule magique, mais comme le seuil d'énergie cinétique nécessaire pour vaincre l'énergie potentielle gravitationnelle d'une planète entière. C'est la base de toute l'astronautique. -
2. Appréhender la Dynamique Orbitale (Mécanique Céleste)
Saisir que dans l'espace, la ligne droite n'existe pas. Vous calculerez des temps de trajet basés sur des orbites de transfert de Hohmann (ellipses tangentes), comprenant ainsi pourquoi on ne peut aller sur Mars que tous les 26 mois (fenêtre de tir) et pourquoi la distance géométrique n'est pas le seul facteur de durée. -
3. Modéliser la Survie en Milieu Hostile
Appliquer des lois mathématiques (exponentielles décroissantes) à des systèmes biologiques. Vous comprendrez comment quantifier la "chance" et le "risque" à travers le temps. C'est une introduction à la biologie quantitative : comment passer d'une observation qualitative ("c'est dangereux") à une prédiction chiffrée ("13,5% de survie"). -
4. Pratiquer l'Analyse Dimensionnelle
Jongler avec des unités très différentes (km/s, années, UA, kg) et vérifier la cohérence de vos résultats. Une erreur d'unité en astrophysique peut mener à des résultats absurdes (ou à des crashs de sondes spatiales !).
Données de l'étude : Le Scénario de l'Impact
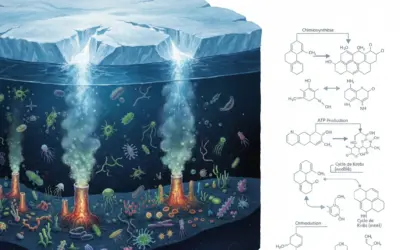
Situation Initiale : Imaginez la scène il y a 3,9 milliards d'années, durant le "Grand Bombardement Tardif". Mars, qui possédait alors probablement des océans et une atmosphère plus dense, est frappée violemment par un astéroïde de plusieurs kilomètres de diamètre. L'énergie libérée est colossale, équivalente à des millions de bombes nucléaires.
Au point d'impact, la roche est vaporisée instantanément. Mais sur les bords du cratère, dans ce qu'on appelle la zone de spallationZone où les ondes de choc s'interfèrent pour éjecter la matière sans la chauffer excessivement., des fragments de la croûte martienne sont éjectés vers le ciel à des vitesses hypersoniques, sans être fondus. Certains de ces fragments contiennent des colonies de bactéries endolithes (vivant à l'intérieur de la roche).
Notre mission est de calculer si ces "astronautes involontaires" ont une chance réaliste d'atteindre la Terre vivants, en traversant le vide interplanétaire.
1. Les Paramètres Physiques de Mars
Pour déterminer si le rocher peut quitter la planète rouge, nous devons connaître son "poids" gravitationnel et la force nécessaire pour s'en arracher. Voici les constantes physiques nécessaires :
| Caractéristique | Symbole | Valeur | Comparaison Terre |
|---|---|---|---|
| Masse de Mars | \(M\) | \(6,39 \times 10^{23} \text{ kg}\) | ~10% de la Terre |
| Rayon moyen | \(R\) | \(3389 \text{ km}\) | ~53% de la Terre |
| Constante gravitationnelle | \(G\) | \(6,67 \times 10^{-11} \text{ m}^3\cdot\text{kg}^{-1}\cdot\text{s}^{-2}\) | Identique (Constante universelle) |
| Distance Mars-Terre (Moyenne) | \(d\) | \(78 \times 10^6 \text{ km}\) | Variable (55 à 400 M km) |
Vue Orbitale (Système Solaire)
Scénario d'Impact (Mars)
2. La Trajectoire de Transfert
Une fois libéré de l'attraction martienne, le rocher devient un petit astéroïde en orbite autour du Soleil. Pour qu'il percute la Terre, il ne peut pas voyager en ligne droite (ce qui demanderait une énergie infinie). Il doit suivre une ellipse de transfert, se laissant "tomber" vers le Soleil jusqu'à croiser l'orbite terrestre. C'est le principe du Transfert de Hohmann, la route la plus économe en énergie.
Trajectoire de Transfert (Hohmann)
| Nom du Paramètre | Symbole | Valeur à Trouver | Unité |
|---|---|---|---|
| Vitesse Libération | \(v_{\text{lib}}\) | ? | \(\text{m/s}\) |
| Temps de voyage | \(t\) | ? | \(\text{années}\) |
3. Problématique et Questions
Nous allons décomposer ce voyage épique en plusieurs étapes critiques pour valider la théorie. C'est une enquête en trois actes : l'évasion, la traversée du désert, et l'atterrissage.
- Défi n°1 : L'Évasion. Le rocher doit atteindre une vitesse suffisante pour ne pas retomber sur Mars. C'est une question de pure énergie cinétique.
- Défi n°2 : La Patience. Le voyage dure longtemps. Les bactéries peuvent-elles survivre à l'exposition aux radiations pendant cette durée ? C'est une question de biologie et de statistiques.
- Défi n°3 : Le Bouclier. Quelle taille doit faire le rocher pour offrir une protection adéquate sans devenir une bombe à l'arrivée ? C'est un problème d'optimisation.
Questions à traiter dans l'exercice :
- Calculer la vitesse de libération théorique de Mars.
- Estimer le temps de voyage minimum en utilisant une orbite de transfert idéale.
- Calculer le taux de survie des bactéries après ce voyage, en tenant compte de la décroissance radioactive naturelle de la population.
- Analyser l'impact du diamètre du fragment rocheux sur la protection et la faisabilité de l'éjection.
- Conclure sur la plausibilité scientifique globale de la panspermie martienne.
Les bases théoriques approfondies
Pour résoudre ce problème de panspermie, nous devons mobiliser des concepts de trois disciplines distinctes : la mécanique newtonienne (pour quitter Mars), la mécanique céleste (pour voyager vers la Terre) et la biologie quantitative (pour survivre au voyage).
1. Mécanique : Le Puits de Potentiel Gravitationnel
Imaginez la gravité d'une planète comme un entonnoir géant dont il faut sortir. Pour s'en échapper définitivement sans moteur (balistique), un objet doit posséder une énergie cinétique initiale au moins égale à l'énergie potentielle gravitationnelle qui le retient. C'est ce qu'on appelle la vitesse de libération (\(v_{\text{lib}}\)).
Si l'objet est lancé moins vite que \(v_{\text{lib}}\), il décrira une ellipse et retombera sur la planète (ou se mettra en orbite). S'il dépasse cette vitesse, sa trajectoire sera une parabole ou une hyperbole, et il s'éloignera à l'infini.
Dérivation par l'Énergie Mécanique
En isolant \(v\), la masse \(m\) de l'objet s'annule (une bactérie doit aller aussi vite qu'une montagne pour s'échapper) :
Où :
- \(G\) : Constante gravitationnelle universelle (la "force" de la gravité dans l'univers).
- \(M\) : Masse de l'astre attracteur (kg). Plus il est lourd, plus il est dur de partir.
- \(R\) : Distance au centre de l'astre (m), ici le rayon de la planète.
2. Biologie : La Cinétique de Mort Cellulaire
Dans un environnement hostile constant (radiations, vide), la mort d'une population bactérienne n'est pas linéaire (elles ne meurent pas toutes en même temps), mais probabiliste. Chaque bactérie a une probabilité constante de mourir à chaque instant \(t\). Cela conduit à une loi de décroissance exponentielle, exactement comme la désintégration radioactive des atomes.
Loi de Survie Exponentielle
Où :
- \(N(t)\) : Nombre de survivants au temps \(t\).
- \(N_0\) : Population initiale (au moment du lancement).
- \(\tau\) (Tau) : La constante de temps ou "temps de vie moyen". C'est la durée au bout de laquelle la population a été divisée par \(e\) (il reste environ 37% de vivants).
Influence du blindage : La valeur de \(\tau\) dépend directement de l'épaisseur du rocher. Un rocher plus épais bloque plus de radiations, augmentant \(\tau\) et donc la durée de survie.
3. Astrodynamique : L'Orbite de Hohmann
Dans l'espace, la ligne droite n'existe pas. Pour aller de Mars à la Terre, on ne "vise" pas la Terre. On se laisse tomber vers le Soleil sur une orbite elliptique calculée pour tangenter l'orbite de Mars au départ et l'orbite de la Terre à l'arrivée. C'est l'orbite de transfert de Hohmann, la plus économe en énergie (\(\Delta v\) minimal).
La durée de ce voyage est régie par la 3ème loi de Kepler, qui lie la taille de l'orbite (demi-grand axe \(a\)) à la durée pour la parcourir (période \(T\)).
3ème Loi de Kepler
Si on exprime les distances en Unités Astronomiques (UA) et le temps en années, cette constante vaut simplement 1, ce qui simplifie énormément les calculs :
Pour un transfert, le demi-grand axe \(a\) est la moyenne des rayons des orbites de départ et d'arrivée : \(a = (r_1 + r_2) / 2\).
Correction : La Lithopanspermie Interplanétaire
Question 1 : Vitesse de Libération de Mars
1. Principe Physique Fondamental
Pour qu'un objet (ici, un fragment rocheux) quitte définitivement la surface d'une planète sans jamais retomber, il doit vaincre l'attraction gravitationnelle de celle-ci. Imaginez la gravité comme un "puits" invisible. Plus la planète est massive, plus le puits est profond.
L'énergie que l'on fournit au départ sous forme de vitesse (Énergie Cinétique \(E_c\)) doit être au moins égale à l'énergie qui retient l'objet au fond du puits (Énergie Potentielle de Gravitation \(E_p\)). C'est un bilan énergétique simple : si vous lancez la pierre assez fort, elle aura assez d'élan pour grimper jusqu'au "bord" du puits (l'infini) et s'en échapper.
2. Mini-Cours : Mécanique Newtonienne
Conservation de l'Énergie Mécanique :
Dans le vide (sans frottements), l'énergie mécanique totale \(E_m\) est conservée.
- \(E_c = \frac{1}{2}mv^2\) (L'énergie du mouvement)
- \(E_p = -\frac{GMm}{R}\) (L'énergie de position gravitationnelle, négative car c'est une énergie de liaison)
La condition de libération correspond au cas limite où l'objet arrive à l'infini avec une vitesse nulle. Donc :
3. Remarque Pédagogique
L'indépendance de la masse : Remarquez que la masse \(m\) du rocher apparaît des deux côtés de l'équation ci-dessus. On peut donc la simplifier ! Cela signifie qu'une petite pierre et une montagne nécessitent exactement la même vitesse pour être éjectées (bien que l'énergie nécessaire pour atteindre cette vitesse soit très différente).
4. Normes et Unités (Système International)
En physique, la cohérence des unités est la clé. La constante de gravitation \(G\) est exprimée en unités SI (mètres, kilogrammes, secondes).
- Les distances doivent être impérativement en mètres (m), pas en kilomètres.
- Les masses en kilogrammes (kg).
- Les vitesses en mètres par seconde (m/s).
5. Formule utilisée
En isolant \(v\) dans l'équation de conservation d'énergie, on obtient la formule de la vitesse de libération (ou vitesse d'évasion) :
6. Hypothèses de travail
Pour que ce modèle soit valide, nous posons :
- Modèle Balistique : L'objet reçoit toute son impulsion au départ (comme un boulet de canon), contrairement à une fusée qui accélère en continu.
- Atmosphère négligée : On suppose que l'atmosphère martienne ne freine pas significativement le rocher (ce qui est vrai pour les gros fragments traversant l'atmosphère fine de Mars très vite).
- Corps isolé : On néglige l'attraction du Soleil et des lunes (Phobos/Deimos) au moment du départ.
7. Données Numériques
| Paramètre | Symbole | Valeur brute | Unité SI |
|---|---|---|---|
| Constante Gravitationnelle | \(G\) | \(6,67 \times 10^{-11}\) | \(\text{SI}\) |
| Masse de Mars | \(M\) | \(6,39 \times 10^{23}\) | \(\text{kg}\) |
| Rayon de Mars | \(R\) | 3389 | \(\text{km}\) |
8. Astuces de Calcul
Gérez les puissances de 10 séparément des nombres décimaux pour éviter les erreurs de saisie sur la calculatrice. Exemple : \((A \cdot 10^x) \times (B \cdot 10^y) = (A \times B) \cdot 10^{x+y}\).
Schémas Situation Initiale
Le Problème Physique
9. Calculs Détaillés
Étape A : Conversion des unités
La première source d'erreur est l'unité du rayon. Il est donné en kilomètres, mais la constante \(G\) est en mètres cubes. Nous devons convertir :
Étape B : Calcul du terme énergétique (Numérateur)
Calculons d'abord le produit \(2GM\), qui représente le double du "paramètre gravitationnel standard" de Mars (\(\mu\)) :
Notez que les puissances s'additionnent : \(-11 + 23 = 12\).
Étape C : Division par le Rayon
Nous divisons maintenant ce potentiel par la distance au centre de la planète (le rayon \(R\)) :
Étape D : Racine Carrée (Résultat final)
Enfin, pour obtenir la vitesse \(v\), nous prenons la racine carrée. N'oubliez pas que \(\sqrt{10^6} = 10^3\) :
Étape E : Conversion finale
Pour que le résultat soit plus parlant, convertissons-le en kilomètres par seconde :
Conclusion : Tout fragment rocheux éjecté à moins de 5,0 km/s retombera sur Mars. C'est la "barrière d'entrée" pour le voyage interplanétaire.
Schémas Validation
Visualisation du Résultat
Il est deux fois plus facile de quitter Mars que de quitter la Terre.
10. Réflexions Physiques
5 km/s, c'est énorme (18 000 km/h). Aucune éruption volcanique ne peut produire une telle vitesse. Seul l'impact d'un astéroïde massif créant une onde de choc hyper-véloce peut accélérer des roches à cette vitesse sans les vaporiser instantanément (dans la zone de spallation).
11. Points de vigilance
Erreur classique : Oublier la racine carrée à la fin du calcul, ce qui donne une vitesse \(v^2\) astronomique (environ 25 millions !).
12. Points à Retenir
- ✅ La vitesse de libération dépend de la densité de la planète (Masse et Rayon).
- ✅ Elle ne dépend pas de la masse de l'objet lancé.
- ✅ C'est une barrière énergétique : c'est le "coût" minimum pour l'espace.
13. Le saviez-vous ?
La Terre possède une vitesse de libération de 11,2 km/s. C'est pourquoi nous trouvons beaucoup de météorites martiennes sur Terre, mais nous n'avons jamais trouvé de météorite terrestre sur Mars (c'est beaucoup plus dur de monter la pente gravitationnelle terrestre).
14. FAQ
Une fusée a-t-elle besoin d'atteindre 5 km/s instantanément ?
Non ! Une fusée a un moteur qui pousse en continu. Elle peut monter doucement à 100 km/h tant qu'elle a du carburant. Mais un caillou éjecté par un impact est un projectile balistique : il n'a pas de moteur. Il doit avoir toute sa vitesse (5 km/s) dès la première seconde, sinon il retombe.
A vous de jouer
Quelle serait la vitesse de libération si Mars était 2 fois plus massive (en km/s, arrondi) ?
📝 Mémo
Plus la planète est petite, plus il est facile de s'en échapper. Mars est une bonne base de lancement.
Question 2 : Estimer le temps de voyage minimum (Orbite de Hohmann)
1. Principe Physique Fondamental : "Surfer" sur la gravité
Contrairement à une voiture ou un avion, un objet dans l'espace ne voyage pas en ligne droite d'un point A à un point B. Pour aller de Mars à la Terre, le rocher (ou un vaisseau spatial) doit se placer sur une orbite elliptique autour du Soleil qui touche à la fois l'orbite de départ (Mars) et l'orbite d'arrivée (Terre).
L'orbite qui demande le moins d'énergie (et donc celle qu'un rocher éjecté a le plus de chance "d'emprunter" naturellement) s'appelle l'Orbite de Transfert de Hohmann. C'est une ellipse qui est tangente à l'orbite de Mars à son point le plus éloigné (aphélie) et tangente à l'orbite de la Terre à son point le plus proche (périhélie). Le rocher se laisse littéralement "tomber" vers le Soleil jusqu'à croiser la Terre.
2. Mini-Cours : La 3ème Loi de Kepler
Loi des Périodes : Johannes Kepler a découvert en 1619 une relation magique qui lie le temps et l'espace pour tout objet en orbite.
Le carré de la période orbitale (\(T^2\), la durée d'un an sur cette orbite) est directement proportionnel au cube du demi-grand axe (\(a^3\), la "taille" moyenne de l'orbite).
Cela signifie que si vous connaissez la taille de votre orbite (\(a\)), vous connaissez automatiquement la durée du voyage (\(T\)).
3. Remarque Pédagogique : Le choix des unités
En physique, on utilise souvent le SI (mètres, secondes). Mais en mécanique céleste, cela donne des chiffres astronomiques illisibles (\(1,49 \times 10^{11} \text{ m}\)).
L'astuce des astronomes : Nous allons utiliser le système d'unités solaires :
- Distance en Unités Astronomiques (UA) : \(1 \text{ UA} = \text{Distance Terre-Soleil}\).
- Temps en Années Terrestres (an).
Dans ce système, pour la Terre, \(a=1\) et \(T=1\). Donc la constante de Kepler vaut \(1^2/1^3 = 1\). La formule devient simplissime : \(T^2 = a^3\) !
4. Normes et Conventions
Par convention pour cet exercice :
• 1 an = 12 mois (approximation suffisante).
• Les orbites des planètes sont considérées comme circulaires (excentricité négligée pour simplifier).
5. Formules utilisées
Pour calculer le temps de trajet, nous procédons en 3 étapes logiques :
A. Taille de l'orbite de transfert (demi-grand axe)
C'est la moyenne arithmétique des rayons des deux planètes.
B. Période orbitale totale (Kepler)
C. Temps de voyage (Aller simple)
6. Hypothèses
Ce calcul suppose une "fenêtre de tir" parfaite : le rocher quitte Mars au moment exact où la Terre est positionnée de telle sorte qu'ils se rencontreront à l'arrivée. C'est le scénario "idéal".
7. Données Numériques
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Distance Terre-Soleil | \(r_{\text{Terre}}\) | 1,00 | \(\text{UA}\) |
| Distance Mars-Soleil | \(r_{\text{Mars}}\) | 1,52 | \(\text{UA}\) |
8. Astuces de Calcul
Sur votre calculatrice, pour calculer \(\sqrt{x^3}\), vous pouvez taper :
• \(x \wedge 1.5\)
• ou \((x \wedge 3) \rightarrow \sqrt{\dots}\)
Schémas Situation Initiale (Avant Calcul)
Configuration de Transfert
9. Calculs Détaillés
Étape A : Calcul de la taille de l'orbite (Demi-grand axe)
L'orbite de transfert est une ellipse qui touche Mars d'un côté et la Terre de l'autre. Son grand axe est donc simplement la somme de la distance Soleil-Mars et Soleil-Terre. Le demi-grand axe \(a\) en est la moitié.
Interprétation : Durant son voyage, le rocher sera en moyenne à 1,26 fois la distance Terre-Soleil.
Étape B : Calcul de la Période Orbitale (Kepler)
Si le rocher faisait un tour complet sur cette orbite (revenant à son point de départ sur Mars), combien de temps cela prendrait-il ? Nous utilisons la loi simplifiée \(T = \sqrt{a^3}\).
D'abord, calculons le cube de la distance :
Ensuite, prenons la racine carrée pour avoir le temps :
Interprétation : Une "année" sur cette orbite de transfert dure environ 1,41 année terrestre.
Étape C : Calcul du Temps de Transit réel
Le rocher ne fait pas un tour complet ! Il parcourt seulement la moitié de l'ellipse pour aller de l'extérieur (Mars) vers l'intérieur (Terre). Nous divisons donc la période par 2.
Étape D : Conversion en mois
Pour mieux visualiser cette durée, convertissons-la en mois (\(1 \text{ an} \approx 12 \text{ mois}\)) :
Conclusion : Le voyage le plus rapide possible entre Mars et la Terre dure environ 8 mois et demi. C'est comparable à la durée de vol des missions spatiales actuelles (comme Curiosity ou Perseverance).
Schémas Validation (Après Calcul)
Résultat Temporel Visualisé
(Minimum théorique pour un transfert balistique)
10. Réflexions Physiques
Ce calcul nous donne la limite inférieure absolue. Dans la réalité, un rocher éjecté par un impact part dans une direction aléatoire avec une vitesse aléatoire. Il ne suit presque jamais cette trajectoire parfaite. Il peut orbiter le Soleil pendant des millions d'années, subissant les perturbations gravitationnelles de Jupiter, avant de finir par percuter la Terre par pur hasard. La moyenne observée pour les météorites martiennes (analyse des rayons cosmiques) est plutôt de l'ordre de quelques millions d'années.
11. Points de vigilance
Erreur classique : Confondre la période de l'orbite complète (\(T\)) avec le temps de trajet (\(T/2\)). Si vous trouvez 1,4 an, c'est que vous avez oublié de diviser par deux ! Vous avez calculé un aller-retour Mars-Terre-Mars.
12. Points à Retenir
- ✅ L'unité Astronomique (UA) simplifie la vie : \(1 \text{ UA} = \text{Terre-Soleil}\).
- ✅ La loi \(T^2 = a^3\) ne marche que si \(T\) est en années et \(a\) en UA.
- ✅ Le transfert de Hohmann est le "toboggan" gravitationnel le plus efficace du système solaire.
13. Le saviez-vous ?
La "fenêtre de tir" pour aller sur Mars (le moment où la Terre et Mars sont bien alignées pour ce transfert) ne s'ouvre que tous les 26 mois. C'est pourquoi les agences spatiales envoient leurs robots par vagues tous les deux ans (2020, 2022, 2024...).
14. FAQ
Peut-on aller plus vite en ligne droite ?
Oui, avec un moteur puissant, on peut forcer une trajectoire plus directe (transfert hyperbolique). Mais un rocher n'a pas de moteur. Il est esclave de la gravité et ne peut que suivre les ellipses de Kepler.
A vous de jouer
Si Mars était située à 4 UA du Soleil, quel serait le temps de transit (années, arrondi 1 décimale) ?
📝 Mémo
Hohmann = Économie max d'énergie, pas Vitesse max.
Question 3 : Calculer le taux de survie des bactéries
1. Principe Biologique : La "Loterie" de la Survie
Dans le vide spatial, les bactéries sont en état de stase (dormance). Elles ne consomment pas d'énergie et ne se réparent pas. Cependant, elles sont bombardées par des particules de haute énergie (rayons cosmiques) qui traversent la roche et brisent leur ADN.
C'est un processus purement probabiliste : à chaque instant, une bactérie a une chance fixe d'être frappée mortellement. Lorsqu'une population subit un taux de mortalité constant sans pouvoir se reproduire, sa diminution suit une loi mathématique précise : la décroissance exponentielle. C'est exactement la même loi qui régit la désintégration radioactive des atomes.
2. Mini-Cours : La Constante de Temps (\(\tau\))
Définition : La constante de temps \(\tau\) (Tau) représente la "résistance" du système. C'est la durée moyenne qu'il faut pour que la population soit divisée par un facteur \(e\) (environ 2,718).
Interprétation physique :
- Si \(t < \tau\) : La majorité survit.
- Si \(t = \tau\) : Il reste \(1/e \approx 37 \%\) de survivants.
- Si \(t > 3\tau\) : Il ne reste presque plus rien (< 5%).
Dans notre cas, \(\tau\) dépend de l'épaisseur du bouclier rocheux : plus le mur est épais, plus \(\tau\) est grand.
3. Remarque Pédagogique
Pourquoi \(e\) ? Le nombre d'Euler (\(e \approx 2,718\)) apparaît naturellement dès qu'une variation est proportionnelle à la quantité actuelle (ici : plus il y a de bactéries, plus il y a de morts par seconde, mais le pourcentage de morts reste constant). C'est la base de toutes les équations d'évolution naturelle.
4. Normes et Unités
Pour calculer l'exposant de l'exponentielle, les unités de temps doivent être identiques. Si \(t\) est en années, \(\tau\) doit être en années. Le rapport \(t/\tau\) est alors un nombre sans dimension (une grandeur physique pure).
5. Formules utilisées
La loi de survie s'écrit :
Loi de décroissance de population
Pour obtenir un pourcentage, on divise par la population initiale \(N_0\) et on multiplie par 100 :
Taux de survie (%)
6. Hypothèses du modèle
Pour que ce calcul soit valide, nous supposons :
- Flux constant : L'intensité des radiations cosmiques est stable sur la durée du voyage (pas de supernova proche).
- Pas de reproduction : Les bactéries sont congelées et inertes. Elles ne peuvent pas compenser les pertes par des naissances.
- Population homogène : Toutes les bactéries ont la même résistance intrinsèque.
7. Données Numériques
| Paramètre | Signification | Valeur |
|---|---|---|
| \(t\) | Durée du voyage (calculée précédemment ou donnée) | \(1\,000\,000 \text{ années}\) |
| \(\tau\) | Constante de survie (protection du rocher) | \(500\,000 \text{ années}\) |
Note : Une valeur de \(\tau = 500\,000 \text{ ans}\) correspond à une protection très efficace (rocher de plusieurs mètres ou bactérie extrêmement résistante).
8. Astuces de Calcul
Sur votre calculatrice, la fonction exponentielle est souvent la touche \(e^x\) (inverse de \(ln\)). N'oubliez pas le signe "moins" dans l'exposant, sinon vous calculerez une invasion bactérienne explosive au lieu d'une extinction !
Schémas Situation Initiale (Avant Calcul)
Population de départ (t=0)
Au lancement, la roche est saturée de vie.
9. Calculs Détaillés
Étape A : Calcul du "facteur de risque" (l'exposant)
Nous devons d'abord comparer la durée du voyage à la capacité de résistance. Nous calculons le rapport \(k = t / \tau\).
Interprétation : Le voyage dure deux fois plus longtemps que la "durée de vie caractéristique" de la colonie. On s'attend donc à une mortalité importante (bien plus que 50%).
Étape B : Calcul de la fraction restante
Nous appliquons maintenant la fonction exponentielle. Nous cherchons la valeur de \(e^{-2}\).
Cela signifie qu'il reste 0,1353 "part" de la population initiale.
Étape C : Conversion en pourcentage
Pour exprimer cela en taux de survie \(S\) :
Schémas Validation (Après Calcul)
Population à l'arrivée (t = 1 million d'années)
10. Réflexions Physiques
Un taux de 13,5% peut sembler faible, mais en microbiologie, c'est énorme. Si le rocher contenait initialement 1 milliard de bactéries (ce qui tient dans un cube de sucre), il en reste 135 millions vivantes à l'arrivée. Il suffit d'une seule bactérie viable tombant dans un océan primordial favorable pour démarrer une biosphère planétaire par reproduction exponentielle.
11. Points de vigilance
Erreur de raisonnement : Ne pensez pas linéairement ! "Si ça dure deux fois \(\tau\), tout le monde est mort". Non. L'exponentielle ne touche jamais zéro mathématiquement. Il reste toujours une fraction infinitésimale de survivants.
12. Points à Retenir
- ✅ La survie dépend du rapport \(t/\tau\).
- ✅ \(\tau\) (la protection) est le paramètre que l'on peut faire varier (en choisissant un plus gros caillou).
- ✅ En biologie des populations, "quelques survivants" = "succès total" grâce à la reproduction ultérieure.
13. Le saviez-vous ?
La bactérie championne de la survie, Deinococcus radiodurans, possède plusieurs copies de son génome. Si les radiations brisent une copie, elle utilise les autres comme "modèle" pour réparer les cassures, comme un puzzle auto-reconstituant.
14. FAQ
Pourquoi ne meurent-elles pas de faim pendant 1 million d'années ?
Parce qu'elles ne vivent pas ! En état de cryptobiose (dessiccation complète), le métabolisme est à l'arrêt (0%). C'est comme une horloge dont on a retiré la pile. Pas de consommation, pas de vieillissement, pas de faim. Seule la destruction physique de la machine (l'ADN) par l'extérieur (radiations) compte.
A vous de jouer
Si le voyage durait \(t = \tau\) (500k ans), quel serait le taux de survie (%, arrondi entier) ?
📝 Mémo
Le temps détruit, mais le nombre protège. La loi des grands nombres est l'alliée de la vie.
Question 4 : Analyser l'impact du diamètre du fragment rocheux
1. Principe Physique : Le Dilemme de la Taille
La taille du fragment rocheux (le "véhicule") est le paramètre critique de la mission. C'est un problème d'optimisation complexe car les contraintes sont contradictoires :
- Contrainte de Protection (Il faut être GROS) : Pour bloquer les radiations cosmiques, il faut de la matière. Plus le mur est épais, mieux on est protégé.
- Contrainte de Survie Thermique (Il faut être GROS) : Lors de l'entrée dans l'atmosphère, la surface fond (ablation). Il faut assez de matière "sacrifiable" pour que le cœur reste intact.
- Contrainte Mécanique (Il faut être PETIT) : Pour être éjecté de Mars à 5 km/s, il faut une énergie colossale. Plus le rocher est lourd, plus il est difficile de l'accélérer sans le pulvériser lors du choc initial. De plus, un énorme astéroïde qui s'écrase sur Terre vaporise tout à l'impact (cratère), tuant les passagers.
2. Mini-Cours : Ablation et Diffusivité Thermique
L'Ablation : Lors d'une rentrée atmosphérique à haute vitesse (v > 11 km/s), l'air devant l'objet est comprimé violemment, créant un plasma à plus de 10 000°C. La surface de la roche fond et se vaporise instantanément. Cette vapeur emporte avec elle l'essentiel de la chaleur. C'est un système de refroidissement par "sacrifice" de matière.
L'Inertie Thermique : La roche (silicates) est un très mauvais conducteur de chaleur. L'onde de chaleur se propage très lentement vers l'intérieur. Comme la traversée de l'atmosphère ne dure que quelques secondes à quelques minutes, la chaleur n'a pas physiquement le temps d'atteindre le centre. C'est le principe de l'"Alaska Omelette" (glace au four).
3. Remarque Pédagogique
La Loi Carré-Cube : C'est un concept fondamental en physique. Si vous doublez la taille d'un objet (x2) :
• Sa surface (protection, ablation) augmente au carré (x4).
• Son volume et sa masse (difficulté d'éjection) augmentent au cube (x8).
Le poids devient vite un problème majeur par rapport au gain de protection.
4. Normes et Conventions
Pour estimer la taille idéale, nous utilisons les valeurs empiriques observées sur les météorites retrouvées sur Terre :
- Perte par ablation : Environ 1 à 5 cm d'épaisseur sur toute la surface (varie selon l'angle d'entrée).
- Épaisseur de blindage anti-radiation : Environ 20 à 40 cm de roche pour réduire la dose de radiation à un niveau survivable sur 1 million d'années.
5. Données : Tableau d'Analyse Comparative
| Catégorie | Diamètre | Protection Radiations | Comportement Rentrée | Verdict |
|---|---|---|---|---|
| Poussière | < 1 mm | Nulle (ADN détruit instantanément par UV) | Vaporisée ou tombe doucement (mais stérile) | IMPOSSIBLE |
| Caillou | 1 cm - 10 cm | Faible (Rayons cosmiques traversent) | Entièrement consumé (étoile filante) | ÉCHEC |
| Rocher (Météorite) | 20 cm - 1 m | Optimale (Cœur protégé) | Croûte de fusion superficielle, cœur froid | IDÉAL |
| Astéroïde | > 10 m | Parfaite | Survivant, mais impact explosif au sol (Cratère) | RISQUÉ (Vaporisation à l'impact) |
6. Astuces de Raisonnement
Pensez à une pomme de terre sortie du feu : la peau est brûlée, la chair sous la peau est bouillante, mais si elle est grosse et qu'elle n'est restée que peu de temps, le centre peut être encore cru. C'est exactement ce qu'on cherche pour nos bactéries.
Schémas Situation Initiale (Comparaison des menaces)
Comparatif de Tailles et Menaces
7. Calculs Logiques (Dimensionnement)
Nous allons dimensionner le rayon minimal \(R_{min}\) nécessaire pour que le cœur reste habitable.
Étape A : Définition des épaisseurs critiques
Étape B : Sommation pour le Rayon
Le rayon total doit inclure la couche sacrifiée (ablation) + la couche de protection restante + le cœur utile.
Étape C : Calcul du Diamètre
Le diamètre est le double du rayon :
Conclusion : Il faut un rocher d'environ un demi-mètre de diamètre (la taille d'un ballon de gym) pour assurer une sécurité maximale.
Schémas Validation (Coupe Transversale Détaillée)
Anatomie d'une météorite habitable
Coupe théorique après atterrissage : L'extérieur est brûlé, mais l'intérieur profond est intact et stérile aux radiations.
10. Réflexions Physiques
Ce dimensionnement explique pourquoi la lithopanspermie est statistiquement difficile mais individuellement robuste. Les "bons" cailloux (taille moyenne) sont moins nombreux que les poussières, mais ce sont les seuls vecteurs viables. La nature filtre les candidats : seuls ceux qui ont la "bonne armure" transmettent la vie.
11. Points de vigilance
Contre-intuition : On pense souvent que l'impact au sol tue tout le monde. C'est faux pour les météorites de taille moyenne. Elles sont freinées par l'atmosphère à haute altitude (vol obscur) et tombent en chute libre terminale à environ 200-300 km/h. C'est un choc violent, mais une bactérie dans une pierre peut survivre à une telle décélération sans problème.
12. Points à Retenir
- ✅ Le diamètre idéal est de l'ordre de 50 cm à 1 mètre.
- ✅ La roche est un isolant thermique exceptionnel (le cœur reste froid).
- ✅ Le freinage atmosphérique permet un atterrissage "relativement" doux pour les passagers microscopiques.
13. Le saviez-vous ?
La météorite martienne ALH84001, célèbre pour ses hypothétiques microfossiles, pèse 1,93 kg. C'est un peu petit pour une protection parfaite sur des millions d'années, mais suffisant pour un transit rapide. La météorite Tissint (tombée au Maroc en 2011) pesait au total environ 7-10 kg avant fragmentation, une taille idéale.
14. FAQ
Si la roche chauffe à 10 000°C, comment l'intérieur reste-t-il froid ?
C'est une question de temps et de conductivité. Imaginez que vous passez votre doigt très vite à travers la flamme d'une bougie. Vous ne vous brûlez pas. La météorite traverse l'atmosphère en quelques secondes/minutes. La chaleur n'a physiquement pas le temps de diffuser (se propager) à travers la pierre, qui conduit mal la chaleur.
A vous de jouer
Quel est le principal danger pour un rocher de 2 cm de diamètre ?
📝 Mémo
Trop petit = grillé. Trop gros = écrasé. Moyen = le vaisseau spatial parfait.
Question 5 : Conclusion sur la plausibilité scientifique
1. Principe Épistémologique : La Chaîne Probabiliste
En science, pour valider une théorie complexe comme la panspermie sans observation directe, on utilise une approche par "maillons faibles". Le voyage de Mars à la Terre est une chaîne d'événements successifs. Pour que la théorie soit valide, il ne suffit pas que l'ensemble soit possible ; il faut que chaque étape individuelle soit physiquement réalisable.
Si la probabilité d'une seule étape est nulle (par exemple, si aucun rocher ne peut résister à l'éjection), alors la probabilité totale est nulle (\(0 \times \dots = 0\)). Notre travail consiste à vérifier qu'aucun "zéro" n'existe dans cette équation.
2. Mini-Cours : Plausibilité vs Preuve
La nuance critique :
- Plausible : Cela signifie que le phénomène respecte toutes les lois connues de la physique, de la chimie et de la biologie. Rien ne l'interdit. C'est un scénario "crédible".
- Prouvé : Cela signifie que nous avons une observation directe ou une trace fossile indiscutable confirmant que cela s'est réellement produit.
La lithopanspermie est aujourd'hui classée comme hautement plausible, mais non prouvée (car nous n'avons pas encore trouvé de "passager" vivant ou fossile dans une météorite martienne de manière incontestée).
3. Remarque Pédagogique
Loi des Grands Nombres : Même si la probabilité qu'un rocher spécifique contienne de la vie et survive est infime (disons une chance sur un milliard), le nombre d'impacts sur Mars durant 4 milliards d'années est astronomique. En multipliant une probabilité très faible par un nombre d'essais gigantesque, l'événement improbable devient statistiquement inévitable.
4. Normes et Critères de Validation
Pour accepter l'hypothèse, nous exigeons :
- Physique : Vitesse d'éjection \(v > 5.0 \text{ km/s}\) possible sans fusion totale.
- Biologie : Survie \(S > 0.001\%\) après un transit moyen.
- Géologie : Existence avérée de météorites martiennes sur Terre.
5. Formule Logique (Équation de type Drake)
Nous pouvons modéliser la probabilité globale \(P_{\text{succès}}\) comme le produit de probabilités conditionnelles :
Tant que chaque terme est strictement supérieur à zéro, le transfert est possible.
6. Hypothèses Finales
Nous supposons pour cette conclusion que :
- La vie existait sur Mars au moment des impacts (c'est la grande inconnue, mais c'est le postulat de l'exercice).
- La vie martienne, si elle existait, était basée sur une chimie (ADN/ARN) compatible avec les conditions de survie que nous connaissons.
7. Synthèse des Résultats (Le Verdict)
| Étape Critique | Verdict | Justification Scientifique |
|---|---|---|
| 1. Éjection | POSSIBLE | La zone de spallation permet d'atteindre \(v > 5 \text{ km/s}\) sans chauffer le cœur de la roche (pression élevée mais température basse). |
| 2. Transit | PROUVÉ | Nous avons plus de 300 météorites martiennes dans nos musées. Le transport de matière est un fait établi. |
| 3. Survie | PLAUSIBLE | Les calculs montrent que 13,5% survivent à 1 million d'années si le rocher fait >20cm. Les spores bactériennes sont incroyablement résistantes. |
| 4. Entrée | POSSIBLE | L'ablation ne touche que la surface. L'intérieur reste froid. Le crash final est amorti par l'atmosphère (vitesse terminale ~300 km/h). |
8. Astuces de Raisonnement
Ne cherchez pas la certitude absolue. En sciences historiques (comme l'origine de la vie), on cherche la "meilleure explication disponible" compatible avec les faits. La lithopanspermie est une excellente candidate car elle résout le problème du temps trop court pour l'apparition de la vie sur Terre.
Schémas Situation Initiale (L'Hypothèse)
Le Grand "? "
Avons-nous une origine commune ?
9. Analyse Finale
L'exercice démontre que le voyage est périlleux mais pas impossible. Le goulot d'étranglement n'est pas le lancement (violent) ni l'arrivée (chaude), mais la durée du transit.
Si une roche met 10 millions d'années à arriver, les radiations auront stérilisé même le cœur le plus profond. Mais si une roche arrive en 10 000 ans (trajectoire rapide), la charge biologique est quasi-intacte. Or, la mécanique céleste nous dit qu'une petite fraction des éjectas arrive très vite (résonances gravitationnelles). C'est cette petite fraction qui suffit à ensemencer un monde.
Schémas Validation (La Connexion)
La Chaîne du Vivant
10. Implications Philosophiques
Si la lithopanspermie est un mécanisme efficace, cela signifie que la vie n'est pas "enfermée" sur sa planète d'origine. Dès que la vie apparaît quelque part, elle a tendance à contaminer tout le système planétaire, pour peu qu'il y ait de l'eau liquide ailleurs.
11. Points de vigilance
Attention au biais : Dire que "c'est possible" ne prouve pas que "c'est arrivé". Pour l'instant, la vie terrestre est la seule que nous connaissons. La panspermie reste une théorie élégante en attente de validation.
12. Points à Retenir
- ✅ Les planètes rocheuses échangent de la matière (météorites).
- ✅ Les micro-organismes peuvent survivre aux trois phases critiques (choc, vide, rentrée).
- ✅ Mars et la Terre sont probablement des "sœurs biologiques".
13. Le saviez-vous ?
Si nous colonisons Mars un jour, nous ferons de la "panspermie dirigée". Nous serons les vecteurs qui amèneront la vie terrestre (nos propres corps et nos bactéries) sur la Planète Rouge, bouclant peut-être la boucle ouverte il y a 4 milliards d'années.
14. FAQ
La vie a-t-elle pu faire le chemin inverse (Terre -> Mars) ?
Absolument. C'est même statistiquement probable après l'impact géant qui a tué les dinosaures (Chicxulub). Des débris terrestres ont été éjectés. Cependant, le puits de gravité terrestre étant plus profond (11,2 km/s), l'éjection est énergétiquement plus difficile que depuis Mars.
A vous de jouer
Si on découvre de la vie sur Mars un jour, quelle sera la première chose à vérifier ?
📝 Mémo
Nous sommes peut-être tous des Martiens... ou les Martiens sont peut-être des Terriens égarés. L'histoire de la vie s'écrit à l'échelle du système solaire.
Analyse pas à pas de l'odyssée
Détail des mécanismes physiques en jeu à chaque étape du schéma ci-dessus.
1 L'Éjection : La zone de spallation
Le voyage commence par un événement d'une violence inouïe. Un astéroïde percute Mars. Dans la zone de spallation (proche de la surface), les ondes de choc se réfléchissent et éjectent la roche vers le haut à une vitesse hypersonique sans la chauffer excessivement.
- Le défi : Les bactéries doivent encaisser une accélération de plusieurs milliers de \(g\).
- La solution : Les micro-organismes, grâce à leur petite taille et leur absence de structures complexes, résistent très bien aux chocs mécaniques intenses.
2 Le Transit : Le froid et le blindage
Dans le vide spatial, l'eau s'évapore et les bactéries entrent en cryptobiose (état de dormance). Elles ne vieillissent presque plus.
- Température : Le froid (-270°C à l'ombre) conserve l'ADN.
- Radiations : C'est le danger principal. Seul un rocher d'au moins 20 cm d'épaisseur peut bloquer suffisamment les Rayons Cosmiques Galactiques pour permettre une survie sur des millénaires.
3 L'Entrée : Le paradoxe thermique
Lors de la rentrée atmosphérique terrestre, la friction crée un plasma à 10 000°C.
- L'Ablation : La surface de la météorite fond et s'évapore, emportant la chaleur avec elle.
- Isolation : La roche est un mauvais conducteur thermique. Le processus est si rapide (quelques secondes) que la chaleur n'a pas le temps de pénétrer au cœur. L'intérieur reste froid !
📝 Grand Mémo : Synthèse Approfondie
Voici l'analyse détaillée des concepts clés qui régissent la théorie de la lithopanspermie, reliant la mécanique céleste à la microbiologie :
-
🚀
1. La Barrière Gravitationnelle (Vitesse de Libération)
La gravité agit comme un "puits" dont il faut s'extraire. Pour Mars, ce ticket de sortie coûte 5,0 km/s d'énergie cinétique pure. Contrairement à une fusée qui accélère progressivement, un fragment rocheux doit acquérir cette vitesse instantanément lors de l'impact initial. Cela implique une violence extrême : seules les ondes de choc générées par des impacts d'astéroïdes massifs peuvent catapulter des tonnes de roches à des vitesses hypersoniques vers l'espace sans les pulvériser totalement (grâce aux zones de spallation). C'est le premier filtre sélectif : peu de roches réussissent ce saut balistique.
-
🛡️
2. Le Concept de "Bunker Naturel" (Protection)
L'espace est un environnement hostile dominé par deux types de radiations mortelles : les ultraviolets (UV) solaires et les Rayons Cosmiques Galactiques (GCR).
• Les UV stérilisent la surface en quelques secondes mais sont arrêtés par une simple feuille de papier (ou quelques microns de poussière).
• Les GCR sont des particules à haute énergie qui traversent la matière comme des balles de fusil, brisant l'ADN.
Pour survivre sur le long terme, les bactéries doivent être des endolithes (vivant à l'intérieur de la pierre). Une épaisseur de roche d'au moins 30 à 50 cm est nécessaire pour atténuer suffisamment les GCR et ramener le taux de mortalité à un niveau acceptable sur des millénaires. Le rocher agit donc comme une capsule spatiale blindée. -
⏳
3. La Course contre la Montre (Facteur Temps)
Le temps est l'ennemi. Même protégée et congelée, une cellule subit une dégradation thermodynamique lente (hydrolyse de l'ADN, racémisation des acides aminés). La survie suit une loi exponentielle décroissante (\(e^{-t/\tau}\)).
• Un transfert direct (type Hohmann) de 8 mois offre une survie quasi-totale.
• Un transfert chaotique de 10 millions d'années réduit la probabilité de survie à presque zéro.
La lithopanspermie repose donc sur une fenêtre statistique : il faut qu'une fraction infime des éjectas trouve la Terre "rapidement" (en quelques millénaires) pour que la charge biologique soit encore viable. -
🌌
4. Changement de Paradigme (Faisabilité)
Cet exercice démontre que les planètes ne sont pas des écosystèmes fermés et isolés ("biens sous cloche"). Il existe un échange de matière continu entre Mars et la Terre (environ 500 kg de Mars tombent sur Terre par an).
Si la vie apparaît sur une planète, la probabilité qu'elle contamine les voisines n'est pas nulle. Cela suggère que si nous trouvons de la vie sur Mars, il y a de fortes chances qu'elle partage une ancêtre commun avec la vie terrestre. Nous ne serions pas deux arbres de vie distincts, mais deux branches d'un même arbre "Solaire".
"Nous sommes peut-être tous des Martiens... ou les Martiens sont peut-être des Terriens égarés. L'histoire de la vie ne s'écrit pas sur une seule planète, mais à l'échelle du système solaire tout entier."
🎛️ Simulateur de Mission : Survie Bactérienne
Ajustez les paramètres de la mission pour voir si vos passagers microbiens survivent au voyage interstellaire à l'intérieur de la météorite.
Paramètres de Vol
Temps passé dans le vide spatial (en milliers d'années).
Épaisseur de roche protégeant le cœur de la météorite.
État de la Colonie
📝 Quiz final : Testez vos connaissances en Exobiologie
5 questions pour valider votre compréhension des mécanismes de transport de la vie.
1. Pourquoi Mars a-t-elle une vitesse de libération (5,0 km/s) plus faible que la Terre (11,2 km/s) ?
2. Quel est le rôle principal du rocher ("météorite") pendant le voyage spatial ?
3. Que se passe-t-il pour les bactéries situées au cœur de la météorite lors de l'entrée atmosphérique ?
4. Quelle durée de voyage offre la meilleure chance de survie (statistiquement) ?
5. Si on trouve de la vie sur Mars avec le même ADN que sur Terre, quelle sera la conclusion la plus probable ?
📚 Glossaire Approfondi
Détail des termes techniques et concepts clés utilisés dans l'étude de la panspermie.
- Panspermie
-
Du grec pan (tout) et sperma (graine). Théorie scientifique proposant que la vie ne soit pas nécessairement apparue isolément sur Terre, mais qu'elle existe dans tout l'Univers et soit distribuée par des vecteurs célestes (comètes, astéroïdes, poussières interstellaires).
Note importante : Elle ne répond pas à la question de l'origine de la vie (abiogenèse), mais déplace simplement le lieu de cette origine. On distingue la panspermie dirigée (intentionnelle par une intelligence) de la panspermie naturelle (notre sujet). - Lithopanspermie
-
Forme spécifique et la plus plausible de panspermie où le "véhicule" de transport est un fragment rocheux (lithos = pierre).
Mécanisme : Un impact violent sur une planète mère éjecte des débris contenant des micro-organismes endolithes (vivant dans la roche). La roche sert de bouclier contre les ultraviolets et les rayons cosmiques, et d'isolant thermique lors de la rentrée atmosphérique sur la planète cible. C'est le scénario privilégié pour un transfert Mars-Terre. - Vitesse de libération
-
Appelée aussi "vitesse d'évasion". C'est la vitesse minimale qu'un projectile balistique (sans moteur) doit atteindre initialement pour s'arracher définitivement à l'attraction gravitationnelle d'un astre.
Formule : \( v = \sqrt{2GM/R} \).
Contexte : Pour Mars, elle est de 5,0 km/s. Tout objet lancé en dessous de cette vitesse finira par retomber sur la surface ou se mettre en orbite fermée. C'est la barrière énergétique principale au voyage interplanétaire naturel. - Extrémophile
-
Organisme (souvent unicellulaire, bactéries ou archées) capable non seulement de survivre mais de proliférer dans des conditions physico-chimiques létales pour la plupart des êtres vivants (l'Homme inclus).
Dans le contexte spatial, on recherche des :- Radiorésistants : Survivent aux radiations ionisantes (ex: Deinococcus radiodurans capable de réparer son ADN pulvérisé).
- Psychrophiles : Aiment le froid extrême (nécessaire pour le transit).
- Xérophiles : Survivent à la dessiccation (manque d'eau) extrême.
- SNC (Météorites)
-
Acronyme désignant les trois familles historiques de météorites martiennes : Shergottites, Nakhlites, et Chassignites.
La Preuve : Leur origine martienne a été prouvée en analysant des bulles de gaz microscopiques piégées dans le verre de la roche (formé lors du choc d'éjection). La composition isotopique de ce gaz correspondait exactement à celle de l'atmosphère de Mars mesurée in situ par les sondes Viking en 1976. C'est la preuve physique irréfutable que des roches voyagent de Mars à la Terre. - Zone de Spallation
-
Concept clé de la mécanique d'impact. C'est une zone géologique située à la surface d'une planète, à la périphérie immédiate d'un point d'impact d'astéroïde.
Le miracle physique : Dans cette zone, l'interférence des ondes de choc permet d'éjecter des fragments de croûte vers l'espace à des vitesses très élevées, mais en leur faisant subir une pression et une température relativement faibles. C'est ce mécanisme qui permet de lancer des roches dans l'espace sans les vaporiser ni "cuire" les bactéries qu'elles contiennent. - Cryptobiose
-
État physiologique de "vie suspendue" ou de dormance extrême. En réponse à un stress environnemental (dessiccation, gel, vide), l'organisme arrête quasi-totalement son métabolisme (moins de 0,01% de l'activité normale).
Application : Il peut rester dans cet état pendant des millénaires, protégeant ses structures cellulaires, et se "réveiller" (reviviscence) dès que les conditions redeviennent favorables (présence d'eau liquide). C'est la clé de la survie temporelle lors du transit.
Feedback
Chargement...





0 commentaires