Le Vent Stellaire et la Perte de Masse
Contexte : L'Astrophysique Stellaire.
Les étoiles, en particulier les plus massives et chaudes, ne sont pas des objets statiques. Elles éjectent continuellement de la matière dans l'espace sous la forme d'un flux de particules appelé vent stellaireUn flux de gaz et de particules chargées (plasma) éjecté de la haute atmosphère d'une étoile.. Ce phénomène, crucial pour l'évolution de l'étoile et l'enrichissement chimique du milieu interstellaire, est particulièrement intense pour les étoiles de type Wolf-Rayet. Cet exercice vise à calculer le taux de perte de masseLa quantité de masse qu'une étoile perd par unité de temps à cause de son vent. Noté Ṁ (M-point). d'une telle étoile.
Remarque Pédagogique : Cet exercice vous apprendra à appliquer l'équation de continuité de la masse dans un contexte astrophysique pour quantifier un phénomène physique fondamental qui sculpte la vie et la mort des étoiles massives.
Objectifs Pédagogiques
- Comprendre le concept de vent stellaire et de perte de masse.
- Appliquer le principe de conservation de la masse à un écoulement sphérique.
- Calculer le taux de perte de masse d'une étoile massive.
- Manipuler les unités astrophysiques courantes (rayon solaire, masse solaire).
Données de l'étude
Fiche Technique de l'Étoile
| Caractéristique | Valeur |
|---|---|
| Type Spectral | Wolf-Rayet (WN5) |
| Température de surface | ~ 80 000 K |
| Masse | ~ 20 \(M_{\odot}\) |
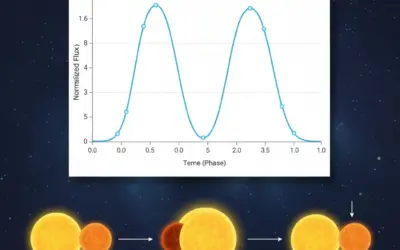
Schéma du Vent Stellaire
| Paramètre Physique | Symbole | Valeur | Unité |
|---|---|---|---|
| Rayon de l'étoile | \(R_{\star}\) | 15 | \(R_{\odot}\) |
| Vitesse terminale du vent | \(v_{\infty}\) | 2000 | km/s |
| Densité du vent à \(10 R_{\star}\) | \(\rho\) | 1.0 \(\times\) 10⁻¹⁵ | g/cm³ |
Questions à traiter
- Convertir le rayon de l'étoile \(R_{\star}\) en mètres (m). On donne \(1 R_{\odot} = 6.96 \times 10^8\) m.
- Convertir la vitesse terminale du vent \(v_{\infty}\) en mètres par seconde (m/s).
- Convertir la densité du vent \(\rho\) en kilogrammes par mètre cube (kg/m³).
- Donner l'expression du taux de perte de masse \(\dot{M}\) pour un vent sphérique stationnaire.
- Calculer le taux de perte de masse \(\dot{M}\) en kg/s. On supposera que le vent a atteint sa vitesse terminale à la distance de \(10 R_{\star}\).
- Exprimer ce taux en masses solaires par an (\(M_{\odot}\)/an). On donne \(1 M_{\odot} = 1.99 \times 10^{30}\) kg et 1 an \(\approx 3.15 \times 10^7\) s.
Les bases sur la Perte de Masse
La perte de masse dans les étoiles est gouvernée par le principe de conservation de la masse. Pour un vent qui s'échappe de manière sphérique et à une vitesse constante (régime stationnaire), la quantité de masse traversant une sphère de rayon \(r\) par seconde est constante.
1. Équation de Continuité
Le taux de perte de masse, noté \(\dot{M}\) (prononcé "M point"), est le produit de la surface de la sphère (\(4\pi r^2\)), de la densité du gaz à cette distance (\(\rho(r)\)) et de la vitesse du gaz (\(v(r)\)).
\[ \dot{M} = 4 \pi r^2 \rho(r) v(r) \]
Cette valeur est constante pour tout rayon \(r\).
2. Vitesse Terminale (\(v_{\infty}\))
Le vent stellaire est accéléré près de la surface de l'étoile. À grande distance, les forces d'accélération s'équilibrent et la vitesse du vent atteint une valeur constante maximale, appelée vitesse terminale et notée \(v_{\infty}\).
Correction : Le Vent Stellaire et la Perte de Masse
Question 1 : Convertir le rayon de l'étoile \(R_{\star}\) en mètres (m).
Principe
Pour garantir la cohérence des calculs physiques, toutes les grandeurs doivent être exprimées dans un système d'unités unique. Nous utilisons le Système International (SI), dont l'unité de longueur est le mètre. Cette étape consiste à traduire la taille de l'étoile, donnée dans une unité astronomique pratique (le rayon solaire), vers l'unité de référence du SI.
Mini-Cours
Le Système International d'unités (SI) est le standard mondial pour la science et l'ingénierie. Il assure que les formules physiques, qui sont des relations entre différentes grandeurs, fonctionnent correctement sans nécessiter de facteurs de conversion supplémentaires. En astrophysique, on utilise souvent des unités "naturelles" comme le rayon solaire (\(R_{\odot}\)) ou la masse solaire (\(M_{\odot}\)) car les nombres manipulés sont plus simples, mais toute application rigoureuse d'une formule physique nécessite un retour au SI.
Remarque Pédagogique
Prenez toujours l'habitude, avant de vous lancer dans un calcul complexe, de lister toutes vos données d'entrée et de les convertir systématiquement dans les unités SI. Cette rigueur initiale vous évitera 90% des erreurs de calcul, notamment celles liées aux ordres de grandeur.
Normes
La référence ici est le Bureau International des Poids et Mesures (BIPM) qui définit les unités du Système International (SI). La valeur du rayon solaire est une constante astronomique standardisée par l'Union Astronomique Internationale (UAI).
Formule(s)
Formule de conversion
Hypothèses
Nous supposons que la valeur du rayon solaire fournie (\(1 R_{\odot} = 6.96 \times 10^8 \text{ m}\)) est une constante suffisamment précise pour cet exercice.
Donnée(s)
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Rayon de l'étoile | \(R_{\star}\) | 15 | \(R_{\odot}\) |
| Conversion Rayon Solaire | \(1 R_{\odot}\) | \(6.96 \times 10^8\) | \(\text{m}\) |
Astuces
Pour un calcul mental rapide, vous pouvez approximer \(6.96 \times 10^8\) par \(7 \times 10^8\). Ainsi, \(15 \times 7 = 105\), ce qui donne un ordre de grandeur de \(105 \times 10^8\) ou \(1.05 \times 10^{10} \text{ m}\), très proche du résultat exact.
Schéma (Avant les calculs)
Conversion d'échelle : Rayon Solaire vers Mètres
Calcul(s)
On multiplie simplement la valeur en rayons solaires par le facteur de conversion.
Schéma (Après les calculs)
Résultat de la Conversion
Réflexions
Le résultat, plus de 10 milliards de mètres, nous donne une idée de l'immensité de cet astre. Cette étoile est 15 fois plus grande en rayon que notre Soleil, ce qui est typique pour une étoile massive en fin de vie.
Points de vigilance
Attention à la manipulation des puissances de 10 lors du passage de \(104.4 \times 10^8\) à l'écriture scientifique \(1.044 \times 10^{10}\). Une erreur d'exposant est vite arrivée.
Points à retenir
Synthèse de la Question 1 :
- Concept Clé : La conversion vers le Système International (SI) est une étape obligatoire avant tout calcul physique.
- Valeur Essentielle : Le rayon solaire vaut approximativement \(7 \times 10^8\) mètres.
Le saviez-vous ?
Comment mesure-t-on le rayon d'une étoile si lointaine ? Pour les étoiles proches, on peut utiliser une technique appelée interférométrie, qui combine la lumière de plusieurs télescopes pour obtenir une résolution angulaire équivalente à celle d'un télescope géant, permettant de "résoudre" le disque de l'étoile et de mesurer son diamètre.
FAQ
Résultat Final
A vous de jouer
Une autre étoile supergéante, Bételgeuse, a un rayon d'environ 887 \(R_{\odot}\). Convertissez cette valeur en mètres.
Question 2 : Convertir la vitesse terminale du vent \(v_{\infty}\) en mètres par seconde (m/s).
Principe
Comme pour la longueur, la vitesse doit être exprimée dans son unité SI, le mètre par seconde (m/s), pour être utilisée dans nos formules physiques.
Mini-Cours
En astronomie, les vitesses radiales (vitesses le long de la ligne de visée) sont mesurées grâce à l'effet Doppler-Fizeau, qui décale les raies spectrales d'un objet. Ce décalage est directement proportionnel à la vitesse. Pour des objets extragalactiques ou des vents stellaires rapides, les vitesses sont si élevées que le km/s est devenu l'unité de facto pour présenter les résultats, mais la conversion en m/s reste nécessaire pour les calculs.
Remarque Pédagogique
La conversion km/s \(\rightarrow\) m/s est simple, mais c'est un bon réflexe de toujours l'écrire pour ne pas l'oublier. L'omettre est une source d'erreur de facteur 1000, ce qui est énorme !
Normes
Le mètre par seconde (m/s) est l'unité de vitesse dérivée du Système International (SI).
Formule(s)
Facteur de conversion
Hypothèses
Aucune hypothèse n'est nécessaire pour une conversion d'unités.
Donnée(s)
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Vitesse terminale | \(v_{\infty}\) | 2000 | \(\text{km/s}\) |
Astuces
Souvenez-vous simplement que "kilo" signifie 1000. Donc, remplacer "km" par "1000 m" est une méthode infaillible.
Schéma (Avant les calculs)
Conversion d'Unité de Vitesse
Calcul(s)
Schéma (Après les calculs)
Vitesse Convertie en m/s
Réflexions
Une vitesse de 2 millions de mètres par seconde est phénoménale. Cela représente 7.2 millions de km/h, soit environ 0.7% de la vitesse de la lumière. Cela illustre l'énergie prodigieuse libérée par ces étoiles massives pour expulser leur propre matière à de telles vitesses.
Points de vigilance
Ne pas confondre km/s et km/h. L'erreur serait un facteur 3600, ce qui changerait radicalement le résultat.
Points à retenir
Synthèse de la Question 2 :
- Concept Clé : Le préfixe "kilo" (k) représente toujours un facteur \(10^3\).
- Application : Le km/s est une unité très courante en astrophysique pour les grandes vitesses.
Le saviez-vous ?
La vitesse du vent solaire de notre propre étoile est bien plus modeste, typiquement entre 300 et 800 km/s. Les vents des étoiles Wolf-Rayet sont parmi les plus rapides et les plus denses connus dans l'Univers.
FAQ
Résultat Final
A vous de jouer
La sonde spatiale Parker Solar Probe a atteint une vitesse record de 163 km/s. Exprimez cette vitesse en m/s.
Question 3 : Convertir la densité du vent \(\rho\) en kilogrammes par mètre cube (kg/m³).
Principe
La densité est une grandeur composée (masse/volume). Sa conversion en unités SI (kg/m³) requiert de convertir à la fois l'unité de masse (gramme \(\rightarrow\) kilogramme) et l'unité de volume (centimètre cube \(\rightarrow\) mètre cube). C'est une double conversion.
Mini-Cours
Lorsqu'on convertit une unité au cube, il faut élever au cube le facteur de conversion de la longueur. Puisque \(1 \text{ m} = 100 \text{ cm} = 10^2 \text{ cm}\), alors \(1 \text{ m}^3 = (10^2 \text{ cm})^3 = 10^6 \text{ cm}^3\). Inversement, \(1 \text{ cm} = 10^{-2} \text{ m}\), donc \(1 \text{ cm}^3 = (10^{-2} \text{ m})^3 = 10^{-6} \text{ m}^3\). C'est une source d'erreur très fréquente.
Remarque Pédagogique
Pour éviter les erreurs sur les unités composées, traitez chaque unité séparément. Convertissez d'abord les grammes en kg, puis les cm³ en m³. Ensuite, combinez les deux résultats. Ne sautez pas d'étapes !
Normes
Le kilogramme par mètre cube (kg/m³) est l'unité de masse volumique du Système International (SI).
Formule(s)
Formule de conversion de densité
Hypothèses
Aucune hypothèse n'est nécessaire.
Donnée(s)
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Densité du vent | \(\rho\) | \(1.0 \times 10^{-15}\) | \(\text{g/cm}^3\) |
Astuces
Retenez simplement que pour passer de g/cm³ à kg/m³, il faut multiplier par 1000. C'est contre-intuitif car on passe d'une "petite" unité (g) à une "grande" (kg), mais le changement sur le volume (cm³ \(\rightarrow\) m³) est beaucoup plus important et domine la conversion.
Schéma (Avant les calculs)
Conversion de Densité : de g/cm³ à kg/m³
Calcul(s)
On applique les deux facteurs de conversion : \(1 \text{ g} = 10^{-3} \text{ kg}\) et \(1 \text{ cm}^3 = 10^{-6} \text{ m}^3\).
Schéma (Après les calculs)
Visualisation de la Densité Résultante
Réflexions
Une densité de \(10^{-12} \text{ kg/m}^3\) est extraordinairement faible. À titre de comparaison, la densité de l'air sur Terre au niveau de la mer est d'environ 1.2 kg/m³. Le vent stellaire, même celui d'une étoile Wolf-Rayet, est des milliards de fois moins dense que l'air que nous respirons. C'est un milieu extrêmement ténu, proche de ce que nous considérons comme un "vide" de laboratoire.
Points de vigilance
L'erreur la plus commune est de se tromper dans l'exposant pour la conversion du volume. Beaucoup d'étudiants utilisent \(10^{-2}\) au lieu de \((10^{-2})^3 = 10^{-6}\).
Points à retenir
Synthèse de la Question 3 :
- Concept Clé : La conversion d'une unité de volume (ou de surface) implique d'élever le facteur de conversion de la longueur à la puissance 3 (ou 2).
- Facteur Clé : \(1 \text{ g/cm}^3 = 1000 \text{ kg/m}^3\).
Le saviez-vous ?
Le meilleur vide que l'on sache créer en laboratoire sur Terre atteint des densités de l'ordre de \(10^{-14}\) kg/m³. Le vent stellaire que nous étudions ici est donc environ 100 fois plus dense que ce vide artificiel ! L'espace interstellaire est "vide", mais pas complètement.
FAQ
Résultat Final
A vous de jouer
La densité de l'eau est de 1 g/cm³. Convertissez cette valeur en kg/m³.
Question 4 : Donner l'expression du taux de perte de masse \(\dot{M}\).
Principe
C'est une application directe de l'équation de continuité pour un écoulement à symétrie sphérique et en régime stationnaire.
Formule(s)
Équation de continuité de la masse
Question 5 : Calculer le taux de perte de masse \(\dot{M}\) en kg/s.
Principe
Le principe physique est la conservation de la masse. La masse qui traverse une coquille sphérique de rayon \(r\) pendant une seconde est simplement la masse contenue dans cette coquille (Surface \(\times\) épaisseur) multipliée par la vitesse. L'épaisseur de la coquille est \(v \times 1\text{s}\). La masse est donc Volume \(\times\) densité \(\Rightarrow\) (\(4 \pi r^2 \times v\)) \(\times \rho\).
Mini-Cours
L'équation \(\dot{M} = 4 \pi r^2 \rho v\) est l'une des équations les plus fondamentales en astrophysique stellaire. Elle relie une quantité macroscopique et globale (\(\dot{M}\), difficile à mesurer directement) à des quantités locales (la densité \(\rho\) et la vitesse \(v\) à un rayon \(r\)) qui peuvent être estimées par l'observation spectroscopique. La constance de \(\dot{M}\) implique que si la vitesse \(v\) augmente avec \(r\), la densité \(\rho\) doit diminuer (et vice-versa) pour que le produit reste constant.
Remarque Pédagogique
Maintenant que toutes les unités sont dans le SI, le calcul est une "simple" application numérique. Concentrez-vous sur l'organisation des termes : regroupez les nombres d'un côté et les puissances de 10 de l'autre pour minimiser les risques d'erreur de calcul.
Normes
Ce calcul ne dépend pas d'une norme d'ingénierie mais du principe fondamental de la conservation de la masse, une des lois de base de la physique.
Formule(s)
Formule du taux de perte de masse
Hypothèses
Nous formulons plusieurs hypothèses simplificatrices :
- Le vent est à symétrie sphérique (identique dans toutes les directions).
- L'écoulement est stationnaire (les propriétés comme \(\rho\) et \(v\) à un rayon \(r\) donné ne changent pas avec le temps).
- À la distance de mesure \(r=10R_{\star}\), le vent a déjà atteint sa vitesse terminale (\(v(r) = v_{\infty}\)).
Donnée(s)
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Rayon de l'étoile | \(R_{\star}\) | \(1.044 \times 10^{10}\) | \(\text{m}\) |
| Densité à \(10 R_{\star}\) | \(\rho\) | \(1.0 \times 10^{-12}\) | \(\text{kg/m}^3\) |
| Vitesse à \(10 R_{\star}\) | \(v_{\infty}\) | \(2 \times 10^6\) | \(\text{m/s}\) |
Astuces
Approximer \(\pi \approx 3.14\) et \(4\pi \approx 12.5\). L'étape de calcul des puissances de 10 est : \(10^{2 \times 11} \times 10^{-12} \times 10^6 = 10^{22 - 12 + 6} = 10^{16}\). Vérifier l'ordre de grandeur final est la meilleure façon de détecter une erreur.
Schéma (Avant les calculs)
Schéma de Calcul pour \(\dot{M}\)
Calcul(s)
Étape 1 : Calcul du rayon de mesure \(r\)
Étape 2 : Appliquer la formule de \(\dot{M}\)
Schéma (Après les calculs)
Visualisation du Flux de Masse
Réflexions
Le résultat est un nombre astronomique : l'étoile perd 274 millions de milliards de kilogrammes chaque seconde ! Cela montre à quel point les processus à l'œuvre dans les étoiles massives sont cataclysmiques, bien au-delà de notre intuition terrestre.
Points de vigilance
L'erreur la plus fréquente ici est d'oublier de mettre le rayon au carré dans la formule \(4 \pi r^2\). Une autre erreur classique est d'utiliser le rayon de l'étoile \(R_{\star}\) au lieu du rayon de mesure \(r = 10 R_{\star}\).
Points à retenir
Synthèse de la Question 5 :
- Concept Clé : La conservation de la masse dans un flux sphérique est la clé.
- Formule Essentielle : \(\dot{M} = 4 \pi r^2 \rho v\) est une formule fondamentale.
- Point de Vigilance : Ne jamais oublier le carré sur le rayon \(r^2\).
Le saviez-vous ?
Les vents stellaires ne sont pas lisses et homogènes. Ils sont en réalité très "grumeleux" (clumpy), avec des surdensités importantes. Si on prend en compte cette structure, les taux de perte de masse estimés peuvent être réduits d'un facteur 2 à 10 par rapport au modèle simple utilisé ici ! C'est un sujet de recherche très actif.
FAQ
Résultat Final
A vous de jouer
Recalculez \(\dot{M}\) (en kg/s) si des mesures plus précises indiquaient une densité deux fois plus faible, soit \(0.5 \times 10^{-12} \text{ kg/m}^3\).
Question 6 : Exprimer ce taux en masses solaires par an (\(M_{\odot}\)/an).
Principe
Le kg/s est une unité SI correcte mais peu intuitive en astrophysique stellaire. On préfère exprimer l'évolution des étoiles en utilisant des unités adaptées à leur échelle : la masse du Soleil (\(M_{\odot}\)) et l'année (an). Cette conversion permet de comparer directement la perte de masse à la masse totale de l'étoile et sur des échelles de temps pertinentes pour son évolution.
Mini-Cours
Le choix des unités est crucial pour l'interprétation d'un résultat. Un taux de perte de masse de \(10^{17} \text{ kg/s}\) est un chiffre énorme qui ne "parle" pas. En le convertissant en \(M_{\odot}/\text{an}\), on peut immédiatement le comparer à la masse de l'étoile (ex: 20 \(M_{\odot}\)) et en déduire une échelle de temps pour la perte de masse : \( \text{Temps} = \frac{\text{Masse}}{\dot{M}} \). Cela donne un sens physique direct au résultat.
Remarque Pédagogique
Cette conversion est un produit/quotient de facteurs. Pour passer de kg à \(M_{\odot}\), on divise par la masse du Soleil en kg. Pour passer de "par seconde" à "par an", on multiplie par le nombre de secondes dans une année.
Normes
La masse solaire (\(M_{\odot}\)) et l'année julienne sont des unités non-SI acceptées pour l'usage en astronomie par l'Union Astronomique Internationale (UAI).
Formule(s)
Formule de conversion du taux de perte de masse
Hypothèses
Nous utilisons les valeurs standards pour la masse solaire et le nombre de secondes dans une année.
Donnée(s)
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Taux de perte de masse | \(\dot{M}\) | \(2.74 \times 10^{17}\) | \(\text{kg/s}\) |
| Masse Solaire | \(M_{\odot}\) | \(1.99 \times 10^{30}\) | \(\text{kg}\) |
| Secondes par an | \(3.15 \times 10^7\) | \(\text{s/an}\) |
Astuces
Le facteur de conversion global est \(\frac{3.15 \times 10^7}{1.99 \times 10^{30}} \approx 1.58 \times 10^{-23}\). Vous pouvez mémoriser ce facteur pour passer rapidement des kg/s aux \(M_{\odot}\)/an.
Schéma (Avant les calculs)
Conversion du Débit Massique
Calcul(s)
Schéma (Après les calculs)
Comparaison de Masse Annuelle
Réflexions
Un taux de \(\sim 4.3 \times 10^{-6} M_{\odot}/\text{an}\) (souvent lu "quatre fois dix moins six masses solaires par an") est considéré comme très élevé. Cela signifie qu'en seulement 1 million d'années (une durée courte pour une étoile massive), elle perdra 4.3 masses solaires, soit près d'un quart de sa masse totale ! Cette perte de masse va modifier sa structure, sa luminosité et déterminer si elle finira sa vie en trou noir ou en étoile à neutrons.
Points de vigilance
L'erreur classique est d'inverser les facteurs de conversion : multiplier par la masse solaire au lieu de diviser, ou diviser par les secondes au lieu de multiplier. Gardez toujours un oeil sur les unités pour vous assurer qu'elles s'annulent correctement.
Points à retenir
Synthèse de la Question 6 :
- Concept Clé : Le choix des unités doit donner un sens physique au résultat.
- Application : Le \(M_{\odot}/\text{an}\) permet de quantifier l'impact de la perte de masse sur l'échelle de temps de l'évolution stellaire.
Le saviez-vous ?
L'étoile la plus extrême connue, R136a1, a une masse de plus de 250 \(M_{\odot}\) et un taux de perte de masse estimé à plus de \(10^{-4} M_{\odot}/\text{an}\). Elle a probablement déjà perdu plus de 50 masses solaires depuis sa naissance, en seulement quelques millions d'années !
FAQ
Résultat Final
A vous de jouer
Le Soleil perd environ \(2 \times 10^9\) kg/s à cause de son vent. Convertissez cette valeur en \(M_{\odot}/\text{an}\).
Outil Interactif : Simulateur de Perte de Masse
Utilisez les curseurs pour voir comment la vitesse du vent et sa densité influencent le taux de perte de masse de l'étoile. Le calcul est effectué pour un rayon fixe de \(10 R_{\star}\).
Paramètres du Vent Stellaire
Résultats Clés
Quiz Final : Testez vos connaissances
1. Quel est le principal moteur des vents stellaires pour les étoiles chaudes et massives ?
2. Comment la perte de masse affecte-t-elle l'évolution d'une étoile massive ?
3. Si la densité du vent \(\rho\) double à rayon constant, comment évolue le taux de perte de masse \(\dot{M}\) ?
4. Le vent de notre Soleil est...
5. L'unité \(M_{\odot}\)/an est une unité de...
- Vent Stellaire
- Un flux de gaz et de particules chargées (plasma) éjecté de la haute atmosphère d'une étoile.
- Taux de Perte de Masse (\(\dot{M}\))
- La quantité de masse qu'une étoile perd par unité de temps à cause de son vent. Typiquement exprimé en masses solaires par an.
- Vitesse Terminale (\(v_{\infty}\))
- La vitesse maximale atteinte par le vent stellaire à grande distance de l'étoile, où l'accélération devient négligeable.
- Masse Solaire (\(M_{\odot}\))
- Une unité de masse standard en astronomie, égale à la masse du Soleil, soit environ \(1.99 \times 10^{30}\) kg.
- Rayon Solaire (\(R_{\odot}\))
- Une unité de distance standard en astronomie, égale au rayon du Soleil, soit environ \(6.96 \times 10^8\) m.
D’autres exercices d’Astrophysique Stellaire:








0 commentaires